Аксіома паралельності Евкліда

1. Рівносильні формулювання постулату про паралельних [ правити | правити код ]
2. Перші начерки неевклідової геометрії [ правити | правити код ]

Аксіома паралельності Евкліда, або п'ятий постулат, - одна з аксіом , Що лежать в основі класичної планіметрії . Вперше наведена в « засадах » Евкліда [1] :

Евклід розрізняє поняття постулат і аксіома , Не пояснюючи їх відмінності; в різних манускриптах «Начал» Евкліда розбиття тверджень на аксіоми і постулати різному, так само як не збігається і їх порядок. У класичному виданні «Начал» Гейберга сформульоване твердження є п'ятим постулатом.

На сучасній мові текст Евкліда можна переформулювати так [2] :

Уточнення, з якою саме сторони перетинаються прямі, Евклід додав, ймовірно, для ясності - легко довести, що воно випливає з самого факту існування перетину [2] .

П'ятий постулат надзвичайно сильно відрізняється від інших постулатів Евкліда, більш простих і очевидних (див. почала Евкліда ). Тому протягом двох тисячоліть не припинялися спроби виключити його зі списку аксіом і вивести як теорему . Всі ці спроби закінчилися невдачею. «Ймовірно, неможливо в науці знайти більш захоплюючу і драматичну історію, ніж історія п'ятого постулату Евкліда» [3] . Незважаючи на негативний результат, ці пошуки не були марними, так як в кінцевому рахунку привели до повного перегляду наукових уявлень про геометрію Всесвіту.

Рівносильні формулювання постулату про паралельних [ правити | правити код ]

У сучасних джерелах зазвичай наводиться інша формулювання постулату про паралельних, рівносильна V постулату і належить Проклу [4] (Її іноді називають аксіомою Плейфера ):

У цьому формулюванні слова «одну і тільки одну» часто замінюють на «тільки одну» або «не більше однієї», так як існування хоча б однієї такої паралельної відразу випливає з теорем 27 і 28 «Начал» Евкліда.

Взагалі у V постулату є величезна кількість рівносильних формулювань, багато з яких самі по собі здаються досить очевидними. Ось деякі з них [5] [6] [7] .

• існує прямокутник (Хоча б один), тобто чотирикутник, у якого всі кути прямі [8] .
• Існують подібні, але не рівні трикутники (аксіома Валліса , 1693 ). І тут досить, щоб існувала хоча б одна пара таких трикутників [8] .
• Будь-яку фігуру можна пропорційно збільшити.
  • Варіант: існує щонайменше одна фігура, яку можна пропорційно збільшити.
• Існує трикутник як завгодно великої площі.
• Пряма, що проходить через точку всередині кута, перетинає принаймні одну його сторону (аксіома Йоганна Фрідріха Лоренца, тисячі сімсот дев'яносто один ).
• Через кожну точку всередині гострого кута завжди можна провести пряму, що перетинає обидві його сторони (одне з припущень Лежандра , 1800 ).
• Зближуються прямі рано чи пізно перетнуться.
  • Варіант: перпендикуляр і похила до однієї і тієї ж прямої неодмінно перетинаються. Затвердження відомо як постулат Лежандра , Хоча це формулювання зустрічалася ще в XIII столітті у ат-Тусі .
• Точки, рівновіддалені від даної прямої (По одну її сторону), утворюють пряму.
  • Варіант: відстань між паралельними прямими завжди постійно, тобто паралельні прямі не можуть ні зближуватися, ні розходитися.
• Якщо дві прямі почали зближуватися, то неможливо, щоб вони потім почали (в ту ж сторону, без перетину) розходитися (аксіома Роберта Сімсона, +1756 ).
  • Варіант: Якщо дві прямі в одну сторону розходяться, то в іншу - зближуються.
• Сума кутів однакова у всіх трикутників.
  • Варіант: існує, як мінімум, одна пара неравновелікіх трикутників з однаковою сумою кутів.
• Існує трикутник (щонайменше один), сума кутів якого дорівнює двом прямим [8] .
• Дві прямі, паралельні третій, паралельні і один одному (аксіома Остроградського , 1 855 ).
• Лінія, ортогональна деякого сімейства паралельних прямих, є прямою.
• Пряма, яка перетинає одну з паралельних прямих, неодмінно перетне і іншу.
• Для будь-якого невиродженого трикутника існує описана окружність (Аксіома Фаркаша Бойяи).
• справедлива теорема Піфагора (Як мінімум в одному прямокутному трикутнику ).
• Відношення довжини кола до її діаметру є константою , Тобто однаково для будь-якої окружності.
• існує окружність (Хоча б одна), у якій відношення довжини окружності до її діаметру одно числу Пі .

равносильность їх означає, що всі вони можуть бути доведені, якщо прийняти V постулат, і навпаки, замінивши V постулат на будь-який з цих тверджень, ми зможемо довести вихідний V постулат як теорему.

Якщо замість V постулату допустити, що для пари точка - пряма V постулат хибний, то отримана система аксіом буде описувати геометрію Лобачевського . Зрозуміло, що в геометрії Лобачевського всі перераховані вище рівносильні твердження невірні.

П'ятий постулат різко виділяється серед інших, цілком очевидних, він більше схожий на складну, неочевидні теорему. Евклід, ймовірно, усвідомлював це, і тому перші 28 пропозицій в «Засадах» доводяться без його допомоги.

«Евклиду безумовно повинні були бути відомі різні форми постулату про паралельних» [4] . Чому ж він вибрав наведену, складну і громіздку? Історики висловлювали різні припущення про причини такого вибору. В. П. Смилга вважав, що Евклід таким формулюванням вказував на те, що дана частина теорії є незавершеною [9] . М. Клайн звертає увагу на те, що п'ятий постулат Евкліда має локальний характер, тобто описує подію на обмеженій ділянці площині, в той час як, наприклад, формулювання Прокла стверджує факт паралельності, який вимагає розгляду всієї нескінченної прямої [10] . Треба пояснити, що античні математики уникали використовувати актуальну нескінченність ; наприклад, другий постулат Евкліда затверджує не нескінченність прямої, а всього лише те, що «пряму можна безперервно продовжувати». З точки зору античних математиків, вищенаведені еквіваленти постулату про паралельних могли здаватися неприйнятними: вони або посилаються на актуальну нескінченність або (ще не введене) поняття вимірювання, або теж не надто очевидні. Ще одну версію висунув історик Імре Той [11] : Евклидова формулювання, можливо, була спочатку (помилково доведеною) теоремою у кого-то з попередників Евкліда, і коли переконалися, що довести її не вдається, статус теореми підвищили до постулату, не змінюючи тексту формулювання.

Якщо зі списку аксіом виключити V постулат, то отримана система аксіом буде описувати так звану абсолютну геометрію . Зокрема, перші 28 теорем «Начал» Евкліда доводяться без використання V постулату і тому відносяться до абсолютної геометрії. Для подальшого відзначимо дві теореми абсолютної геометрії:

• Паралельні прямі існують; це випливає з теорем 27 і 28 «Начал» Евкліда.
• При продовженні двох прямих від точки їх перетину відстань між ними необмежено зростає [12] .

Математики з давніх часів намагалися «поліпшити Евкліда» - або виключити п'ятий постулат з числа вихідних тверджень, тобто довести його, спираючись на інші постулати і аксіоми, або замінити його іншим, настільки ж очевидним, як інші постулати. Надію на досяжність цього результату підтримувало те, що IV постулат Евкліда (всі прямі кути рівні) дійсно виявився зайвим - він був строго доведений як теорема і виключений з переліку аксіом [5] .

За два тисячоліття було запропоновано багато доказів п'ятого постулату, але в кожному з них рано чи пізно виявлявся порочне коло : Виявлялося, що серед явних або неявних посилок міститься твердження, яке не вдається довести без використання того ж п'ятого постулату.

Прокл ( V століття н. е.) в «Коментарі до I книзі Почав Евкліда» повідомляє, що такий доказ запропонував Клавдій Птолемей , Критикує його доказ і пропонує своє власне [12] . У кілька спрощеному вигляді його можна описати так: нехай пряма b {\ displaystyle b} проходить через задану точку A {\ displaystyle A} паралельно прямий a {\ displaystyle a} ; доведемо, що будь-яка інша пряма c {\ displaystyle c} , Проведена через ту ж точку, перетинається з прямою a {\ displaystyle a} . Як згадувалося вище, відстань між прямими від точки їх перетину зростає необмежено (ще раз підкреслимо, що доказ цієї теореми не спирається на V постулат). Але тоді в кінці кінців відстань між c {\ displaystyle c} і b {\ displaystyle b} перевищить відстань між паралельними прямими, тобто прямі c {\ displaystyle c} і a {\ displaystyle a} перетнуться.

Наведене доказ спирається на припущення, що відстань між двома паралельними прямими постійно (або, принаймні, обмежена). Згодом з'ясувалося, що це припущення рівносильне V постулату.

Посидоний (I століття до нашої ери) запропонував визначити паралельні як прямі, на всьому протязі рівновіддалені один від одного. З такого визначення легко виводиться п'ятий постулат. Однак визначення Посидонія некоректно: нізвідки не випливає, що лінія, рівновіддалених від даної прямої, є пряма [13] .

Після занепаду античної культури V постулатом зайнялися математики країн ісламу. Доведення ал-Джаухарі , учня ал-Хорезмі ( IX століття ) [14] , Неявно передбачало: якщо при перетині двох прямих будь-якої третьої навхрест-лежачі кути рівні, то той же має місце при перетині тих же двох прямих будь-який інший. І це припущення рівносильне V постулату.

Сабіт ібн Куррі ( IX століття ) Дав два докази; в першому він спирається на припущення, що якщо дві прямі віддаляються один від одного з одного боку, вони обов'язково наближаються з іншого боку. У другому, як і Посидоний, він виходить з існування рівновіддалених прямих, причому цей факт ібн Куррі намагається вивести з уявлення про «простому русі», т. Е. Про рівномірний рух на фіксованій відстані від прямої (йому представляється очевидним, що траєкторія такого руху - теж пряма) [15] . Кожне з двох згаданих тверджень Ібн Куррі рівносильно V постулату.

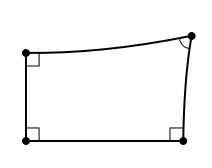
чотирикутник Ламберта

Аналогічну помилку зробив Ібн Аль-Хайсам , Але він вперше розглянув фігуру, пізніше отримала назву « чотирикутник Ламберта »- чотирикутник, у якого три внутрішніх кута - прямі. Він сформулював три можливих варіанти для четвертого кута: гострий, прямий, тупий. Обговорення цих трьох гіпотез, в різних варіантах, багаторазово виникало в пізніших дослідженнях.

Поет і математик Омар Хайям піддав критиці спроби ввести в геометрію механічний рух. Він запропонував замінити V постулат на інший, більш простий: дві сходяться прямі перетинаються, і неможливо, щоб дві сходяться прямі розходилися в напрямі сходження. Кожна з двох частин цього твердження рівносильна постулату Евкліда [16] .

Ал-Абхарі запропонував доказ, схоже на доказом ал-Джаухарі . Це доказ наводить у своїй книзі ас-Самарканд , І ряд дослідників вважав його автором самого ас-Самарканд. Докази походять з вірного в абсолютній геометрії твердження про те, що для будь-якої прямої, що перетинає сторони даного кута, може бути побудована ще одна пряма, яка перетинає сторони цього ж кута і віддалена від його вершини далі, ніж перша. Але з цього твердження автор робить логічно необгрунтовану висновок про те, що через будь-яку точку всередині даного кута можна провести пряму, що перетинає обидві сторони цього кута, - і засновує на цьому останньому твердженні, еквівалентному V постулату, все подальше доказ.

Насир ад-Дін ат-Тусі запропонував побудова, аналогічне побудови Омара Хайяма [17] . Відзначимо, що твори ат-Тусі стали відомі Джон Валліс , І тим самим зіграли роль в розгортанні досліджень по неевклідової геометрії в Європі.

Першу в Європі відому нам спробу докази аксіоми паралельності Евкліда запропонував жив в Провансі (Франція) Герсонід (Він же Леві бен Гершем, XIV століття ). Його доказ спиралося на твердження про існування прямокутника [18] .

До XVI століття відноситься доказ вченого-єзуїта Христофора Клавіуса . Доказ його, як і у ібн Куррі, грунтувалося на твердженні, що лінія, рівновіддалених від прямої - теж пряма [19] .

Валліс в 1693 році в одній зі своїх робіт відтворює переклад твору ат-Тусі і пропонує рівносильну, але більш просте формулювання: існують подібні, але не рівні фігури [20] . Клод Клеро в своїх «Засадах геометрії» ( 1741 ), Як і Герсонід, замість V постулату взяв його еквівалент «існує прямокутник».

В цілому можна сказати, що всі перераховані спроби принесли чималу користь: було встановлено зв'язок між V постулатом і іншими твердженнями, були чітко сформульовані дві альтернативи V постулату - гіпотези гострого і тупого кута.

Перші начерки неевклідової геометрії [ правити | правити код ]

Глибоке дослідження V постулату, засноване на абсолютно оригінальному принципі, провів в 1733 році італійський монах-єзуїт, викладач математики Джироламо Саккери . Він опублікував працю під назвою «Евклід, очищений від усіх плям, або ж геометрична спроба встановити найперші початку всієї геометрії». Ідея Саккери полягала в тому, щоб замінити V постулат протилежним твердженням, вивести з нової системи аксіом якомога більше наслідків, тим самим побудувавши «помилкову геометрію», і знайти в цій геометрії протиріччя або свідомо неприйнятні положення. Тоді справедливість V постулату буде доведена від противного [21] .

Саккери розглядає все ті ж три гіпотези про 4-м вугіллі чотирикутника Ламберта. Гіпотезу тупого кута він відкинув відразу з формальних міркувань. Легко показати, що в цьому випадку взагалі все прямі перетинаються, а тоді можна зробити висновок, що V постулат Евкліда справедливий - адже він як раз і стверджує, що при деяких умовах прямі перетинаються. Звідси робиться висновок, що «гіпотеза тупого кута завжди цілком помилкова, оскільки вона сама себе руйнує» [22] .

Після цього Саккери переходить до спростування «гіпотези гострого кута», і тут його дослідження набагато цікавіше. Він допускає, що вона вірна, і, одне за іншим, доводить цілий ряд наслідків. Сам того не підозрюючи, він просувається досить далеко в побудові геометрії Лобачевського . Багато теорем, доведених Саккери, виглядають інтуїтивно неприйнятними, але він продовжує ланцюжок теорем. Нарешті, Саккери доводить, що в «помилкової геометрії» будь-які дві прямі або перетинаються, або мають загальний перпендикуляр, по обидва боки від якого вони віддаляються один від одного, або ж віддаляються один від одного з одного боку і необмежено зближуються з іншого. У цьому місці Саккери робить несподіваний висновок: «гіпотеза гострого кута абсолютно помилкова, оскільки суперечить природі прямої лінії» [23] .

Мабуть, Саккери відчував необгрунтованість цього «докази», тому що дослідження триває. він розглядає еквідістанту - геометричне місце точок площини, рівновіддалених від прямої; на відміну від своїх попередників, Саккери розуміє, що в даному випадку це зовсім не пряма. Однак, обчислюючи довжину її дуги, Саккери припускається помилки і приходить до реального протиріччя, після чого закінчує дослідження і з полегшенням заявляє, що він «вирвав цю шкідливу гіпотезу з коренем». На жаль, піонерська робота Саккери, видана посмертно, не звернула на себе тієї уваги математиків, якого заслуговувала, і тільки через 150 років ( 1889 ) Його співвітчизник Бельтрами виявив цей забутий працю і оцінив його історичне значення.

В другій половині XVIII століття було опубліковано понад 50 робіт з теорії паралельних. В огляді тих років ( Г. С. Клюгель ) Досліджується більше 30 спроб довести V постулат і доводиться їх хибність. Відомий німецький математик і фізик І. Г. Ламберт , З яким Клюгель листувався, теж зацікавився проблемою; його «Теорія паралельних ліній» була видана (як і праця Саккери, посмертно) в 1786 році .

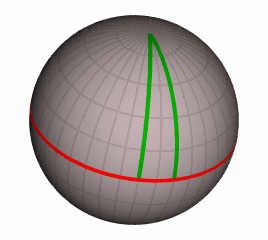
Сферична геометрія: всі прямі перетинаються

Ламберт першим виявив, що «геометрія тупого кута» реалізується на сфері , Якщо під прямими розуміти великі кола . Він, як і Саккери, вивів з «гіпотези гострого кута» безліч наслідків, причому просунувся набагато далі Саккери; зокрема, він виявив, що додаток суми кутів трикутника до 180 ° пропорційно площі трикутника.

У своїй книзі Ламберт проникливо зазначив [24] :

Ламберт не знайшов протиріччя в гіпотезі гострого кута і прийшов до висновку, що всі спроби довести V постулат безнадійні. Він не висловив жодних сумнівів у хибності «геометрії гострого кута», проте, судячи по іншому його проникливого зауваженням, Ламберт розмірковував про можливу фізичну реальності неевклідової геометрії і про наслідки цього для науки [25] :

Чудова робота Ламберта, як і книга Саккери, далеко випередила свій час і не викликала інтересу у тодішніх математиків. Та ж доля спіткала «астральну геометрію» німецьких математиків Ф. К. Швейкарт ( 1817 ) і Ф. А. Таурінус ( тисяча вісімсот двадцять шість ), За ідеями близьку до побудованої Ламбертом.

Тим часом спроби «змити плями» з Евкліда тривали (Луї Бертран, Лежандр , Семен Гур'єв та інші). Лежандр дав цілих три докази V постулату, хибність яких швидко показали його сучасники [26] . Останнє «доказ» він опублікував в 1823 році , За три роки до першої доповіді Лобачевського про нову геометрії.

У першій половіні XIX століття по шляху, прокладеному Саккери, ПІШЛИ К. Ф. Гаусс , Я. Бойяи , Н. І. Лобачевського и Ф. К. Швейкарт . Альо мета у них булу Вже Інша - НЕ роздягнув неевклідову геометрію як Неможливо, а, навпаки, побудуваті альтернативну геометрію и з'ясувати ее можливий роль у реальному мире. На тій момент це булу абсолютно єретічна ідея; ніхто з учених раніше не сумнівався, що фізичний простір евклидово. Цікаво, що Гаусса і Лобачевського навчав в молодості один і той же вчитель - Мартін Бартельс , Який, втім, сам неевклідової геометрією не займався.

Першим був Швейкарт. У 1818 році він відправив Гауса лист з серйозним аналізом основ неевклідової геометрії, проте утримався від винесення своїх поглядів на публічне обговорення. Гаусс теж не зважився опублікувати роботу на цю тему, але його чорнові нотатки та кілька листів однозначно засвідчують глибоке розуміння неевклідової геометрії. Ось кілька характерних уривків з листів Гаусса, де вперше в науці з'являється термін « неевклидова геометрія » [27] :

В 1818 году в листі до австрійського астроному Герлинген Гаусс висловив свої побоювання [29] :

Ознайомившись з роботою Лобачевського «Геометричні дослідження з теорії паралельних», Гаусс енергійно клопоче про обрання російського математика іноземним членом-кореспондентом Геттінгенського королівського товариства (що і сталося в 1842 році ).

Лобачевський і Бойяи проявили велику сміливість, ніж Гаус, і майже одночасно (Лобачевський - в доповіді 1826 року і публікації 1829 року ; Бойяи - в листі 1831 року і публікації 1832 року ), Незалежно один від одного, опублікували виклад того, що зараз називається геометрією Лобачевського . Лобачевський просунувся в дослідженні нової геометрії найдалі, і вона зараз носить його ім'я. Але головна його заслуга не в цьому, а в тому, що він повірив у нову геометрію і мав мужність відстоювати своє переконання (він навіть запропонував експериментально перевірити V постулат, вимірявши суму кутів трикутника) [30] .

У вступі до своєї книги «Нові початку геометрії» Лобачевський рішуче заявляє [31] :

Трагічна доля Лобачевського, підданого остракізму в науковому світі і службовому оточенні за надто сміливі думки, показала, що побоювання Гаусса не були марними. Але і його боротьба була не марна. За іронією долі торжество сміливих ідей Лобачевського забезпечив (посмертно) обережний Гаусс. У 1860-і роки було опубліковано листування Гаусса, в тому числі кілька захоплених відгуків про геометрію Лобачевського, і це привернуло увагу до праць російського математика. У 1868 році вийшла стаття Е. Бельтрамі , Який показав, що площину Лобачевського має постійну негативну кривизну (У евклідової площини кривизна нульова, у СФЕРИ - позитивна); дуже швидко неевклідова геометрія придбала легальний науковий статус, хоча все ще розглядалася як чисто умоглядна [32] .

В кінці XIX-початку XX століття спочатку математики ( Бернхард Ріман , Вільям Кліфорд ), А потім і фізики ( Загальна теорія відносності , Ейнштейн ), Остаточно покінчили з догматом про геометрії Евкліда фізичного простору.

Незалежність п'ятого постулату означає, що його заперечення чи не суперечить іншим аксіомам геометрії (за умови що геометрія Евкліда несуперечлива). Одночасно це означає несуперечливість геометрії Лобачевського . Насправді вірна наступна теорема [33] .

Теорема. Геометрія Лобачевського несуперечлива тоді і тільки тоді, коли несуперечлива евклідова геометрія.

Для доведення цієї теореми в сучасній математиці використовуються моделі однієї геометрії в інший. У моделі для точок, прямих і інших об'єктів першої геометрії будуються об'єкти в рамках другої геометрії так, що для побудованих об'єктів виконуються аксіоми першої. Таким чином, якби протиріччя знайшлося в першій системі аксіом, то воно знайшлося б і в другій.

Складно точно вказати, хто і коли довів цю теорему.

У певному сенсі можна вважати, що це було зроблено вже Лобачевским. Дійсно, Лобачевський зауважив, що геометрія орисфере в просторі Лобачевського є нічим іншим, як Евклідовій площиною; таким чином, існування суперечності в геометрії Евкліда тягло б протиріччя в геометрії Лобачевського [34] . На сучасній мові, Лобачевський побудував модель евклідової площини в просторі Лобачевського. У зворотний бік його побудова йшло аналітично, і несуперечливість геометрії Лобачевського слідувала з несуперечності речового аналізу.

Незважаючи на наявність цих інструментів, Лобачевський НЕ формулював саму теорему несуперечності. Для її суворої формулювання був необхідний логічний аналіз підстав геометрії , Зроблений пізніше оремо , Гильбертом і іншими [33] .

Появою концепції моделі ми зобов'язані Бельтрами . У 1868 році він побудував проектну модель , конформно-евклидову модель , А також локальну модель на так званій псевдосфері . Бельтрами також був першим, хто побачив зв'язок геометрії Лобачевського з диференціальної геометрії.

Побудовані Бельтрами моделі були розвинені пізніше Клейном и Пуанкаре , Завдяки їм побудова було значно спрощено, і також були виявлені зв'язку та додатки нової геометрії до проективної геометрії и комплексного аналізу . Ці моделі переконливо доводять, що заперечення V постулату який суперечить іншим аксіомам геометрії; звідси випливає, що V постулат незалежний від інших аксіом і довести його неможливо [32] .

Як показано вище, додавання п'ятого постулату або його заперечення до решти аксіом Евкліда формує геометрію Евкліда або геометрію Лобачевського відповідно. Для інших поширених однорідних геометрій роль п'ятого постулату не настільки велика.

система аксіом сферічної геометрії вимагає більш суттєвої переробки аксіом Евкліда, оскільки в ній немає паралельних прямих [35] . В проективної геометрії можна визначити паралельні прямі як прямі, які перетинаються тільки в нескінченно віддаленій точці; тоді п'ятий постулат стає простим наслідком аксіоми: «через дві точки можна провести одну і тільки одну пряму». Справді, якщо задати пряму L і точку P поза нею і потім застосувати зазначену аксіому для P і нескінченно віддаленої точки, то отримана пряма буде паралельна L і, очевидно, визначена однозначно [36] .

1. ↑ почала Евкліда / Переклад з грецької та коментарі Д. Д. Мордухай-Болтовського при редакційному участю М. Я. Вигодський і І. Н. Веселовського. - М.-Л .: ГТТІ, 1948. - Т. I. - С. 15. архівна копія від 6 квітня 2008 року на Wayback Machine
2. ↑ 1 2 Каган. Лобачевський, 1948 , С. 164-165.
3. ↑ Смилга, 1988 , С. 4.
4. ↑ 1 2 Історія математики / Під редакцією А. П. Юшкевича , В трьох томах. - М.: Наука, 1970. - Т. I. - С. 110.
5. ↑ 1 2 Мордухай-Болтовской Д. Д. Коментарі до «Початкам» Евкліда, книги I-VI. Указ. соч. - С. 241-244.
6. ↑ Euclid's Fifth Postulate
7. ↑ Каган. Лобачевський, 1948 , С. 167-175.
8. ↑ 1 2 3 Лелон-Ферран Ж., 1989 , С. 255-256.
9. ↑ Смилга, 1988 , С. 59-61.
10. ↑ Клайн М. Математика. втрата визначеності . - М.: Мир, 1984. - С. 94-95. Читальний зал 12 лютого 2007 року. архівна копія від 12 лютого 2007 на Wayback Machine
11. ↑ Tóth I. Das Parallelenproblem im Corpus Aristotelicum // Archive for history of exact sciences . - Berlin-Heidelberg-New York, 1967. - Т. 3, вип. 4,5. - С. 249-422.
12. ↑ 1 2 Смилга, 1988 , С. 72.
13. ↑ Лаптєв Б. Л. Н. І. Лобачевського и его геометрія. - М.: Просвещение, 1976. - С. 71. - 112 с.
14. ↑ Історія математики / Під редакцією А. П. Юшкевича , В трьох томах. - М.: Наука, 1970. - Т. I. - С. 231.
15. ↑ Ібн Корра. Книга про те, що дві лінії, проведені під кутом, меншим двох прямих, зустрічаються / Переклад і примітки Б. А. Розенфельда. - М.: ІМІ, 1963. - Т. XV. - С. 363-380.
16. ↑ Хаййам. Трактати / Переклад Б. А. Розенфельда. Редакція В. С. Сегаля і А. П. Юшкевича. Стаття і коментарі Б. А. Розенфельда та А. П. Юшкевича. - М., 1962.
17. ↑ Ат-Тусі. Трактат, який лікує сумнів з приводу паралельних ліній / Переклад Б. А. Розенфельда, примітки Б. А. Розенфельда та А. П. Юшкевича. - М.: ІМІ, 1960. - Т. XIII. - С. 483-532.
18. ↑ Розенфельд Б. А. Докази п'ятого постулату Евкліда середньовічних математіків Хасана Ібн ал-Хайсама и Льва Герсоніда. - М .: ІМІ, 1958. - Т. XI. - С. 733-742.
19. ↑ Clavius C. Euclidis Elementorum, libri XV. - Romae, +1574.
20. ↑ Wallis. Opera mathematica, v. II. - Oxoniae, 1693. - С. 665.
21. ↑ Історія математики / Під редакцією А. П. Юшкевича , В трьох томах. - М.: Наука, 1972. - Т. III. - С. 215-217.
22. ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. - Leipzig, 1895. - С. 100.
23. ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. - Leipzig, 1895. - С. 105.
24. ↑ Lambert JH Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. - Berlin, 1781-1784. - С. 202-203.
25. ↑ Смилга, 1988 , С. 121.
26. ↑ Історія математики, том III, стор. 218.
27. ↑ Про підстави геометрії, стор. 101-120.
28. ↑ З іншого листа випливає, що постійна дорівнює 1 / - k {\ displaystyle 1 / {\ sqrt {-k}}} , Де k {\ displaystyle k} позначає кривизну .
29. ↑ Про підстави геометрії, с. 119-120.
30. ↑ Лобачевський Н. І. Твори по геометрії (Полн. Собр. Соч., Тт. 1-3). - М. - Л .: ГІТТЛ, 1946-1949.
31. ↑ Про підстави геометрії, с. 61-62.
32. ↑ 1 2 Arcozzi, Nicola. Beltrami's models of non-euclidean geometry (Англ.). Дата звернення 16 липня 2016.
33. ↑ 1 2 Погорєлов А. В. Підстави геометрії. - Изд. 4-е. - М.: Наука, 1979. - С. 18-21. - 152 с.
34. ↑ дивись пункт 34 в Lobachevsky, NI Geometrische Untersuchungen zur Theorie der Parallellinien (нім.). - Berlin: F. Fincke, 1840.
35. ↑ Peil, Timothy. Hilbert's Axioms Modified for Plane Elliptic Geometry (Англ.). // Survey of Geometry. Дата обігу 18 жовтня 2016.
36. ↑ Вольберг О. А. Основні ідеї проективної гегметріі. - Изд. 3-е. - М.-Л .: Учпедгиз РРФСР, 1949. - С. 7. - 188 с.

• Почала Евкліда / Переклад з грецької та коментарі Д. Д. Мордухай-Болтовського при редакційному участю М. Я. Вигодський і І. Н. Веселовського. - М.-Л .: ГТТІ, 1948.
• Вілейтнер Г. Історія математики від Декарта до середини XIX століття . - М.: ГІФМЛ, 1960. - 468 с.
• Гільберт Д. підстави геометрії . - Л.: Сівач, 1923. - 152 с.
• Історія математики з найдавніших часів до початку XIX століття . - М.: Наука, 1972.
• Каган В. Ф. Геометрія Лобачевського і її передісторія. - М.-Л., 1949.
• Каган В. Ф. Лобачевського . - Видання друге, доповнене. - М.-Л .: АН СРСР, 1948. - 507 с.
• Лелон-Ферран Ж. Підстави геометрії. - М.: Мир, 1989. - 312 с. - ISBN 5-03-001008-4 .
• Про Підстави геометрії. Збірник Класичний робіт по геометрії Лобачевського и розвитку ее Ідей. - М., 1956.
• Розенфельд Б. А. Історія неевклідової геометрії: Розвиток поняття про геометричному просторі. - М.: Наука, 1976.
• Розенфельд Б. А. , Юшкевич А. П. Теорія паралельних ліній на середньовічному Сході. - М.: Наука, 1983.
• Смилга В. П. У гонитві за красою. Цікаве введення в неевклідову геометрію. - 2-е вид. - М.: Молодая гвардия, 1988. - 288 с. - ( Еврика ).
• Успенський В. А. Апологія математики. Глава 8. Паралельні прямі - в міфології, реальності та математики . - М.: Амфора, 2009. - ISBN 978-5-367-00689-6 .