В якому тоді сенсі простір може бути неевклідовим? Ім'я Евкліда збереглося б в століттях навіть в тому випадку, якщо б він не зробив нічого, крім введення свого п'ятого постулату (названого пізніше «постулатом про паралельні прямі»). Постулат звучить так: «... якщо пряма, яка перетинає дві інші прямі, утворює з ними на одній стороні внутрішні кути, сума яких менше двох прямих кутів, то ці дві прямі, продовжені до нескінченності, перетнуться стій боку, з якою сума кутів була менше двох прямих ». В іншому формулюванні цей постулат означає, що в заданій площині через задану точку можна провести тільки одну пряму, паралельну заданої прямої. (Існування хоча б одній прямій, паралельної заданої, є наслідком інших постулатів.) Евклід передчував, що цей постулат необхідний, наприклад, для доведення теореми про суму кутів трикутника. Після Евкліда він став предметом суперечок, що тривали протягом багатьох століть. Геометри, починаючи з Птолемея і Прокла та закінчуючи математиками дев'ятнадцятого століття, намагалися довести, що п'ятий постулат є наслідок інших чотирьох.
Ці труднощі пояснюються тим, що людське мислення прагне прив'язатися до простору, яке саме по собі евклидово і складається з фізичних стрижнів і точок, що задовольняють постулату про паралельні прямі. Тільки в дев'ятнадцятому столітті, коли Лобачевський і Бояи показали, що можна побудувати замкнуту геометричну систему, в якій через дану точку проходять кілька прямих, паралельних заданій, стало ясно, що п'ятий постулат є незалежним.
До кінця дев'ятнадцятого століття були створені дві системи неевклідової геометрії. Перша з них - ріманова геометрія - є геометрія на поверхні сфери. У цьому випадку не можна провести жодної прямої, паралельної заданої. Прямі визначені тут як лінії, що проходять через полюси сфери. Друга - це геометрія Лобачевського і Бояи, в якій підтверджується, що через точку можна провести багато прямих, паралельних даній.
Як же все-таки встановити, в якому просторі ми живемо - Евклідовому або неевклідовий? Можливо, що найпростіше це зробити, скориставшись безпосереднім наслідком постулату про паралельні прямі. В геометрії Рімана, або геометрії на поверхні сфери, сума кутів трикутника більше 180 °, причому відміну від 180 ° росте зі збільшенням розмірів трикутника. В геометрії Евкліда ця сума точно дорівнює 180 °, а в геометрії Лобачевського вона менше 180 °. Отже, потрібно просто взяти трикутник (як можна великих розмірів), сторони якого складаються з тих ліній, які в природі вважаються прямими, і визначити, більше або менше 180 ° сума його кутів. Такий експеримент був вперше запропонований Швейкарт. Гаусс спробував визначити, використовуючи звичайний метод тріангуляції і топографічні прилади, дорівнює сума кутів трикутника 180 ° чи ні. За допомогою цих вимірювань, проведених для трикутника, вершини якого утворювали три гори, розташовані на відстанях приблизно 100 км один від одного, Гауса не вдалося помітити ніяких відхилень від 180 °.
Щоб визначити, чи є промені світла Евклідовому прямими, були проведені вимірювання, в яких в якості вершин трикутників використовувалися нерухомі зірки. Наприклад, Лобачевський вимірював кути трикутника, основа якого збігалося з діаметром земної орбіти, а вершина перебувала в місці положення Сіріуса. І знову ніяких відхилень від 180 ° не було виявлено. Лобачевський писав:
«Проте нова геометрія, основи якої закладені в цій роботі, хоча і непріложіма до явищ природи, але може бути об'єктом нашої уяви; не будучи використовуваної в реальних вимірах, вона відкриває нову, область для додатків геометрії до математичного аналізу і навпаки ».
Однак навіть трикутник, утворений діаметром земної орбіти і зіркою Сиріус, малий в порівнянні з трикутниками, які можна вписати у всю відому нам Всесвіт. І можливо, що вимірювання кутів такого гігантського трикутника, сторони якого утворені світловими променями, покажуть, що їх сума більше або менше 180 °. Припустимо, що ми зробили зйомку променями світла, що йдуть від одного кінця Всесвіту до іншого, і виявили, що сума кутів трикутника відрізняється від 180 °, повинні ми тоді зробити висновок, що наш простір неевклидова? Виявляється, що ні. Наш висновок буде повністю залежати від обраної точки зору.
Знову припустимо, що ми прив'язані до двовимірної поверхні сфери і не можемо її покинути. Далі уявімо, що траєкторії світлових променів або натягнуті струни в цьому світі повторюють форму поверхні сфери, утворюючи великі кола. Якби на поверхні цієї сфери ми провели триангуляційні вимірювання за допомогою, наприклад, світлових променів, то ми б виявили, що сума кутів трикутника більше 180 °. У такому випадку, як зазначив Пуанкаре, ми могли б висловити дві різні точки зору. Перша - що ми живемо в неевклідовий просторі, т. Е. В просторі, в якому не можна провести жодної прямої, паралельної заданої. Друга - що ми просто неправильно вибрали прямі лінії, т. Е. Що світлові промені або натягнуті струни, які ми вважали прямими, насправді викривлені і тому не мають властивості евклідових об'єктів.
Поглянувши зовні на поверхню нашої сфери, яка знаходиться в тривимірному евклідовому просторі, ми відразу ж виявимо, що маємо справу з кривими на поверхні сфери, а не з «справжніми» прямими. Тому ми можемо встати на ту точку зору, що «справжнє» простір евклидово, нонам так пощастило (або не пощастило), що ми живемо на поверхні сфери, яка не дозволяє нам реалізувати такі об'єкти (прямі), які мають властивості евклідових об'єктів і задовольняють постулатам Евкліда.
Отже, питання -є чи простір евклідовим чи ні-стає питанням угоди. Якщо ми, наприклад, вирішимо, що промені світла поширюються по прямих лініях, а потім з вимірів виявимо, що сума кутів трикутника, утвореного цими променями, відрізняється від 180 °, ми можемо відмовитися вважати промені світла прямими і спробувати замінити їх чимось іншим . Ясно, що ми завжди вправі так вчинити; саме ця можливість і є джерелом більшості проблем, пов'язаних з питанням про Евклідовому простору.
Якщо з якої-небудь нової фізичної теорії випливає неевклідової простору, то її можна інтерпретувати, вважаючи, що в світі, в якому ми живемо, такі речі, як траєкторії світлових променів, не володіють властивостями евклідових прямих.
Труднощі такої інтерпретації (якщо ми бажаємо допустити, що світлові промені поширюються криволинейно) виникають через те, що в принципі ми можемо собі уявити наш світ, в якому поширюється світло, зануреним у простір, де прямі лінії існують. Так, якщо світло поширюється по поверхні сфери, можна уявити, що ця сфера занурена в тривимірне евклідів простір. В результаті «справжнє» простір виявиться евклідовим. Нам же просто не пощастило, що ми живемо на поверхні сфери.
До тих пір, поки суперечка стосується -лише угоди, жодна з сторін спору не зможе взяти верх. Однак фізична теорія, яка спирається на неевклідової простору, містить в собі щось більше, ніж просто угоду. Вона стверджує, що угода вважати простір евклідовим навряд чи є плідним. Який сенс, наприклад, вважати евклідовим таке простір, в якому світлові промені поширюються так, ніби вони рухаються уздовж поверхні сфери; якщо натягнуті струни згинаються, як ніби вони лежать на цій поверхні; якщо надані самим собі частки переміщаються як би уздовж цієї поверхні; якщо в кінці кінців взагалі неможливо реалізувати такі об'єкти, які мали б властивостями евклідових прямих? Звичайно, при бажанні ми все-таки можемо вважати наш простір евклідовим, але воно буде таким евклідовому простором, в якому виявиться неможливим реалізувати об'єкти, що володіють Евклідовому властивостями. Проявивши впертість, ми все ж можемо назвати «справжнє» простір евклідовим. Однак така інтерпретація буде ще менш плідною.

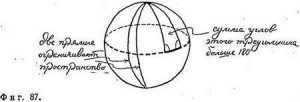
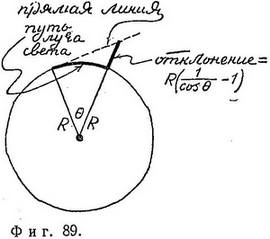
Таким чином, якщо наша діяльність обмежена поверхнею сфери, то простіше (але необов'язково) вважати простір неевклідовим, що володіє властивостями геометрії на сфері, ніж говорити, що ми живемо в такому евклідовому просторі, в якому неможливо реалізувати прямі лінії. Якби вся наша діяльність була обмежена поверхнею сфери, якби світлові промені і т. Д. Рухалися вздовж ліній, зображених на фіг. 87, то в такому світі дві «прямі» замикали б частину простору, сума кутів «трикутника» була б більше 180 ° і т. Д. Ми могли б вважати, що простір «насправді» евклидово, але світло, на жаль, не поширюється в ньому по прямій лінії і відхиляється від «істинної прямий» на величину, що залежить від довжини шляху (фіг. 88). Цю величину можна визначити за такою формулою (фіг. 89): 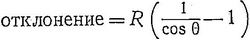
В такому світі ваш колега не здивувався б, якби ви нагадали йому: «Добре відомо, що промені світла (як і все інше) не поширюються прямолінійно. Для побудови прямої необхідно спроектувати промінь світла, а потім підправити його напрямок ».
Теорії тяжіння Ньютона і Ейнштейна (загальна теорія відносності) розрізняються між-собою головним чином поглядом на геометричні властивості простору і часу. У теорії Ньютона вважається, що простір евклидово, а частинки можуть рухатися криволинейно тільки під дією сил. У загальній же теорії відносності передбачається, що простір-час неевклидова, а частинки завжди переміщаються уздовж шляхів, які при заданій кривизні простору збігаються з лініями, найкоротших відстаней між будь-якими двома точками. Хоча ці погляди істотно розходяться, результати обох теорій в більшості випадків практично збігаються - це зайвий раз показує, до якої міри умовний вибір точки зору. Цей вибір визначається виключно тим, наскільки плідні результати тієї чи іншої угоди. Кожна така угода - плід людської думки, і його адекватність дійсного світу перевіряється по тому, наскільки успішно з його допомогою можна організувати явища природи.
Пуанкаре вірив, що найбільш зручним угодою є угода про Евклідовому простору, однак через всього лише 15 років Ейнштейн запропонував свою загальну теорію відносності, в якій він стверджував неевклідової простору. Проте її навряд чи можна вважати «зручнішою». Загальна теорія відносності, хоча і вражає своєю красою та вишуканістю, ніколи не була «зручною» теорією. Численні спроби розрахунків з використанням неевклідової геометрії давали лише малі поправки до результатів теорії Ньютона, яка, без сумніву, більш «зручна», так як евклідова геометрія набагато простіше, ніж будь-яка інша.
В якому тоді сенсі простір може бути неевклідовим?Як же все-таки встановити, в якому просторі ми живемо - Евклідовому або неевклідовий?

